~11 min read
Building Our Own Post-Quantum FIDO Token

Introduction
At Neodyme, we are always careful when it comes to cyber security hypes. Claims about an attack class being eliminated by a single technology oftentimes boil down to a too-good-to-be-true marketing fad. However, one fairly recent development has won us over: FIDO2. FIDO2 is a convenient and phishing-resistant way to do user authentication based on digital signatures. We use FIDO2 for our authentication needs and are quite happy with the implementations we employ.
Yet, recently, for some reason, we decided that was not enough. True to the hacker mindset, we wanted to deep dive into the subject matter by building our very own FIDO2 authenticator — and making it quantum secure using post-quantum crypto (PQC).
This blog post details our journey to a proof-of-concept FIDO2 hardware authenticator. We’ll share insights into our design rationale, provide implementation details and present performance benchmarks. We conclude by comparing our solution to the one Google engineers presented a while ago — and show that it outperforms their approach.
But first things first. Let’s start with some background on FIDO2 and the ongoing post-quantum race.
Fast IDentity Online 2
Fast IDentity Online 2 (FIDO2) is a set of intertwined standards that, when combined, allow for secure user authentication. Relevant for us are the following three standards: FIDO UAF, CTAP2 and Webauthn.
The FIDO Universal Authentication Framework (UAF) provides the foundation for understanding FIDO2: what it is, what it aims to achieve, and how it is intended to be used. On a high level, FIDO2 requires users to possess an authenticator. The authenticator’s role is to securely store cryptographic key material and to sign authentication requests on behalf of the user.
Authenticators generally fall into two categories: roaming or platform. Roaming authenticators are independent of the end user’s device. Common examples include hardware tokens such as Yubikeys, Solokeys or Nitrokeys. Platform authenticators, on the other hand, are built directly into the user’s device, for example the Titan Chip in recent Android smartphones.
Both kinds of authenticator serve the same purpose: Depending on the configuration, they either check for user presence (e.g., by requesting a tap) or verify the user’s identity (e.g., with a fingerprint) before signing an application’s login request. The signing operation is carried out with a private key that is securely stored inside the authenticator.
More recently, password managers such as 1Password or Bitwarden have introduced support for FIDO2-based authentication. However, as we don’t recommend relying solely on software-only authenticators, we will not cover those further.
Within FIDO2, there are three communication parties: Authenticator, the client and the relying party. The picture below shows a common FIDO2 setup including these parties. For web applications, the relying party commonly communicates with the client using Webauthn.
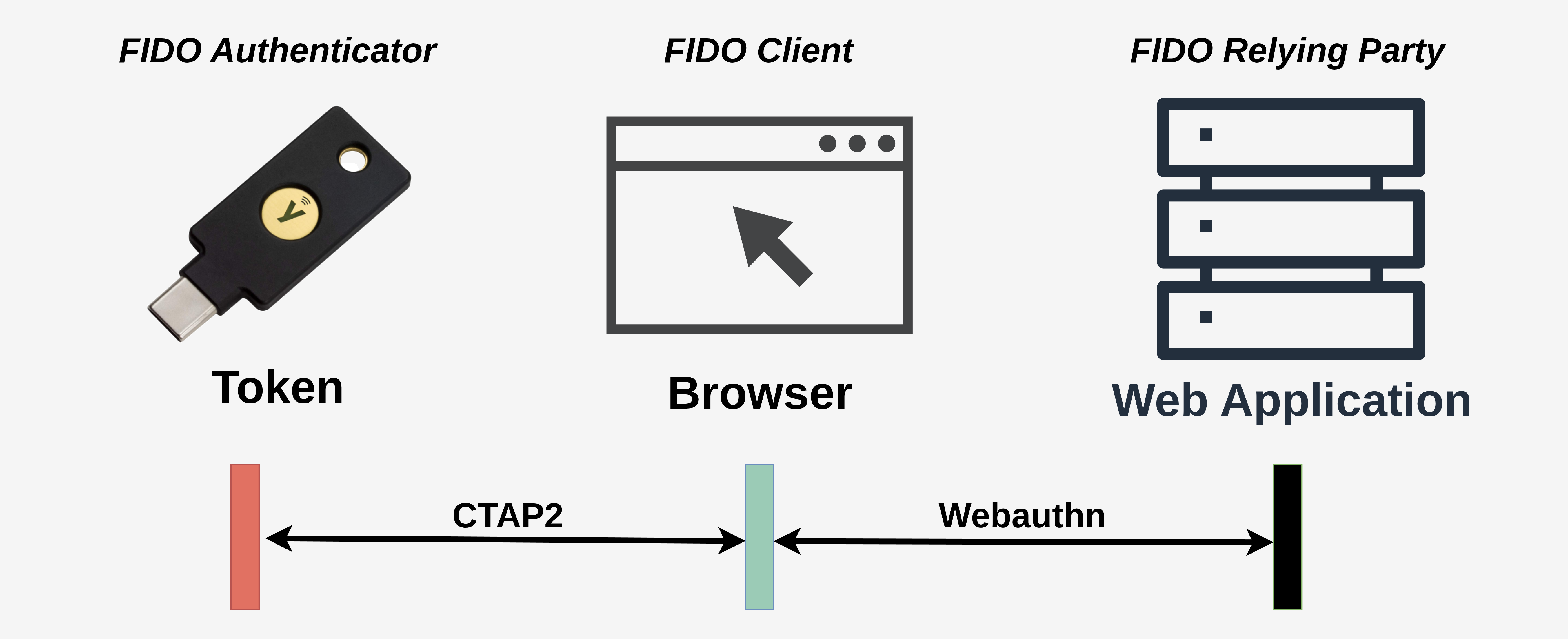
Communication parties involved in FIDO2 authentication
Authenticators communicate exclusively with the client, using the Client to Authenticator Protocol version 2 (CTAP2). The client is typically a piece of software, commonly the web browser or operating system, which acts as the intermediary between the authenticator and the relying party. A relying party is usually a web application that requires user authentication. To build our own authenticator, we therefore need a CTAP2 implementation.
FIDO2 has many configuration options! If you are curious about them, go checkout the spec. For our purposes, what matters is that users authenticate themselves by signing login data. To enable this, the user registers a public key with the relying party. During registration, two main storage options exist: In the resident key setting, only the public key is stored in the application. In the non-resident key setting, the encrypted private key is stored alongside the public key. The FIDO2 standard explicitly allows the application to store this encrypted private key as part of its metadata.
The following informal message flow chart illustrates these differences. In the diagram, symmetric keys are shown in blue, while asymmetric singing keys appear in red.
Registration of credentials within FIDO: Resident vs. non-resident key.
The advantage of non-resident key is that nothing needs to be stored in the authenticator besides a single symmetric key. This is of course very cheap in terms of storage, as a symmetric key is usually between 16 and 32 bytes long. A resident key, on the other hand, has the big advantage that the authenticator knows the credentials per relying party prior to the login. This allows for password-less (and even username-less) authentication. The recently hyped Passkeys employ FIDO2 in the resident key setting for this purpose.
We want our authenticator to allow for both resident and non-resident key scenarios.
Post-Quantum Crypto
FIDO2 is nice and we’d like to continue using it. But, so far, you can use it either with elliptic curve or RSA-based signatures. This can become problematic, as both of those signature flavours might soon be obliterated by quantum computers.
NIST recognized the quantum threat in 2015 and soon after launched a multi-year standardization effort to identify so called post-quantum cryptography schemes. In 2022, NIST selected one key encapsulation mechanism and three signature algorithms for standardization.
The three standardized PQC signature algorithms rely on different assumptions. Dilithium’s and Falcon’s security claims are based on the difficulty of solving large instances of structured-lattice problems. These claims are much discussed and sometimes contested in the academic discourse. Because of these debates and the novelty of the algorithms, most implementers, such as Google, Cloudflare, Signal or Apple, chose to use lattice-based PQC only in conjunction with a pre-quantum algorithm. This ensures that even if the PQC algorithm contains a major flaw, a pre-quantum attacker will not be able to exploit the system. Combining pre- and post-quantum algorithms into so-called hybrid constructions is therefore quite common. However, also hybrid constructions are debated. Famously, in 2022, the National Security Agency (NSA) even stated that it “does not expect to approve” hybrid constructions for national security, citing complexity, interoperability and maintenance concerns.
An entirely different class of PQC signature is the third standardized algorithm: SPHINCS+. SPHINCS+ is hash-based. Its security relies only on well-understood assumptions of the utilized hash primitive. As these assumptions are easier to analyze than their lattice-based counterparts, it does not seem to suffer from the same trust issues. Exemplary of this is the French Cybersecurity Agency’s (ANSSI) position paper on PQC, stating “any product that includes post-quantum mitigation shall implement hybridation except if the quantum mitigation only relies on hash-based signatures like […] SPHINCS+ […]“. The German Federal Office for Information Security (BSI) comes to the same conclusion.
So, by including SPHINCS+ into our authenticator, we could avoid hybridization. But would that work? Let’s first look into what SPHINCS+ is and how it compares to the other standardized PQC algorithms.
SPHINCS+
SPHINCS+ is a stateless hash-based signature scheme. It’s mainly built on the ideas of the Extended Merkle Signature Scheme (XMSS). In essence, that means that signing and verification operations exclusively utilize a cryptographic hash function for constructing hash trees. No crazy elliptic curve, expander graph or lattice mathematics involved! Just a plain and simple hash function, with well understood assumptions.
So SPHINCS+ is a very conservative PQC choice, nice. Where is the catch? Well, the downside of SPHINCS+ can be seen in the next table. The table compares different signature algorithms (in NIST security level ) and their size and performance on a Cortex-M4 processor. As you can see, SPHINCS+ has huge signatures and is very slow.
| Algorithm | Post-Quantum? | Private Key (bytes) | Public Key (bytes) | Signature (bytes) | Keygen (Kcycles) | Sign (Kcycles) | Verify (Kcycles) |
|---|---|---|---|---|---|---|---|
| Ed25519 | ❌ | 32 | 32 | 64 | 200 | 240 | 720 |
| Dilithium2 | ✅ | 2,528 | 1,312 | 2,420 | 1,874 | 7,925 | 2,063 |
| Falcon-512 | ✅ | 1,281 | 897 | 666 | 229,742 | 62,255 | 834 |
| SPHINCS+-128 | ✅ | 64 | 32 | 17,088 | 50,505 | 1,182,422 | 70,501 |
This is why Google engineers didn’t event consider it for FIDO2 in their paper Hybrid Post-Quantum Signatures in Hardware Security Keys, where they implemented FIDO2 with a Dilithium elliptic curve hybrid.
The Challenge
To build our novel, quantum-secure, FIDO2 hardware token, we’d like to have comparable (or better) performance than the Google solution. At the same time we would like to avoid hybridization. We can do this by relying only on hash-based crypto.
To accomplish all this, we need to somehow make SPHINCS+ faster and have smaller signatures than Dilithium in this setting. So, let’s get started.
Implementation
We’ll use the same hardware platform as the Google experiment, a NORDIC nRF52840 employing a Cortex-M4 embedded processor. Cortex-M4 designs are common in TPMs, so its a realistic choice for a roaming authenticator. We’ll also use the same software stack: the OpenSK FIDO2 open-source security key firmware. For our benchmarking we will only consider USB transport, since NFC is scawwy.
Requirements
The requirements for our roaming authenticator come from the FIDO2 spec. One of them is actually already covered by plain-and-standard SPHINCS+. We want:
- ✅ small private and public keys
- ❌ fast signing (=fast login)
- ❌ signatures that fit into a CTAP2 frame (7609 bytes)
So, is there actually something we can do about point 2 & 3? Turns out: Yes. Because SPHINCS+ isn’t actually a signature scheme.
Aligning SPHINCS+
In fact, it is a framework for creating signature schemes. SPHINCS+ provides seven configurable parameters for constructing a signature scheme. Most of these parameters control aspects such as tree heights and widths, and they allow tuning the trade-off between signature size and computational efficiency. If you’re interested in the specifics of how these parameters work and how we optimized them, take a look at our paper linked below.
The figure below illustrates the structure of a SPHINCS+ signature. Each parameter shapes this structure and directly impacts the performance of the scheme.
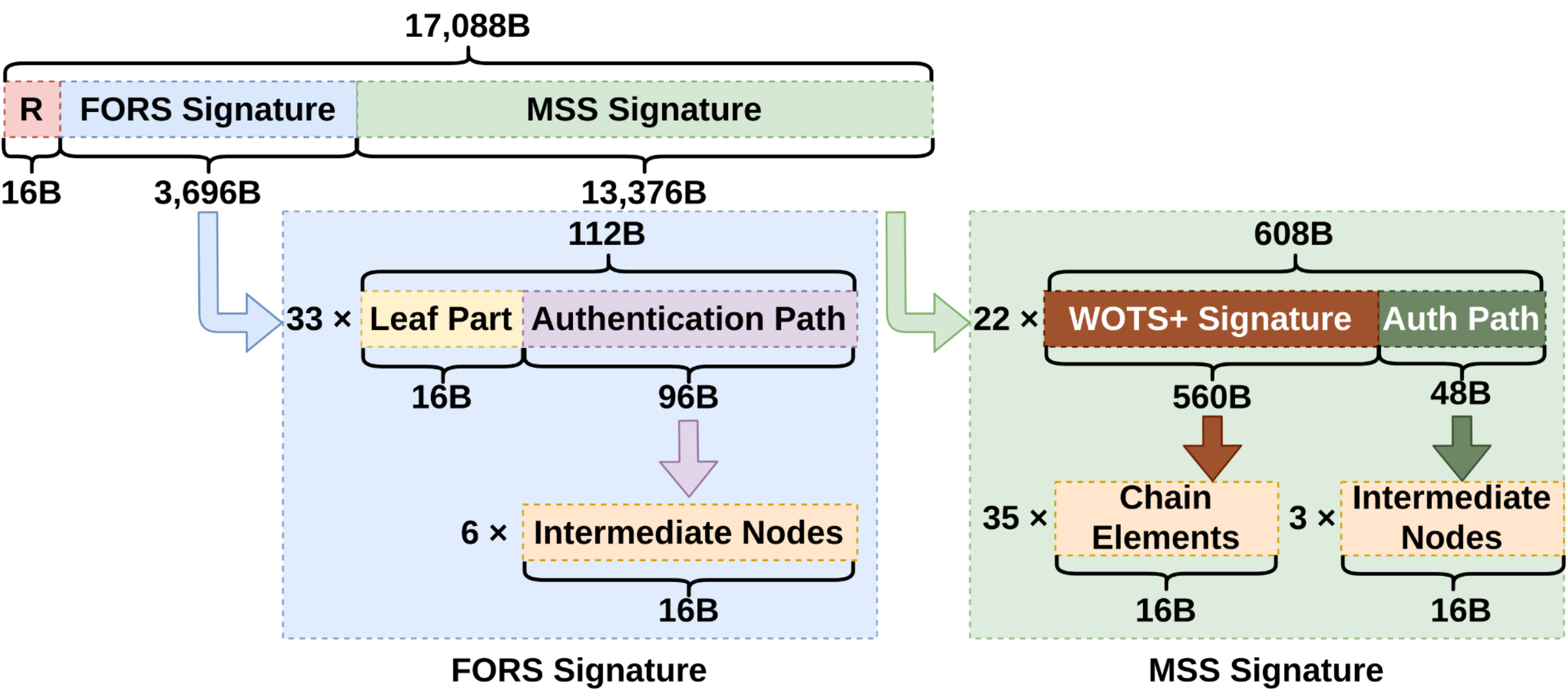
A SPHINCS+ signature unrolled.
Tuning security parameters of an asymmetric algorithm sounds scary. But it is OK actually, as the security of SPHINCS+ can be reduced to that of the utilized hash function. This makes it possible to tie all parameters together with the following not-too-difficult equation. It computes the generic bit security given a quantum computer:
An important parameter for our FIDO2 use case is . It captures the number of allowed signatures per private key. That is: If you generate more signatures than with a single key, security would degrade. NIST defined this value as in its standard. Given we use our FIDO2 authenticator once per day, setting , we could use our authenticator for over a trillion years. Usually not fans of planned obsolescence, here we have to say: This might be overkill.
Lowering this parameter to a more realistic value can yield significant performance improvements. FIDO2 is particularly well-suited for reducing , since each signing operation must be manually confirmed, typically with a simple tap. This makes scenarios involving millions of logins per day impractical. For our token we will experiment with , and . Once a is reached, our authenticator has to generate a new key and store the public key in the relying party, which requires an additional tap. The authenticator, of course, has to keep track of this number.
Implementing CTAP2 with SPHINCS+
In order to run our FIDO2 experiments with SPHINCS+, we had to align the OpenSK CTAP2 open-source firmware. Actually, aligning might be an overstatement. Since we do not require a hybrid construction, we can simply replace the call to the elliptic curve signature code with that of SPHINCS+. To achieve this, we implemented a Rust wrapper around the SPHINCS+ reference implementation, as OpenSK is written in Rust.
We have published a meta-repository that brings together all the resources needed to run our code here. Feel free to explore and experiment with it. Please note, however, that this is a proof of concept, not production-ready code, and should be used at your own risk.
The Results
On modern desktop and server CPUs, lattice-based approaches are orders of magnitude faster than hash-based constructions like SPHINCS+. So we were quite curious to see how our FIDO2-aligned SPHINCS+ would perform on a microcontroller in comparison to Dilithium. We weren’t disappointed.
The following table shows the timings in milliseconds (averaged over 1000 runs) required to complete the CTAP2 commands to make a new credential (MakeCredential) and get a login signature (GetAssertion). Each table contains results from the Google research paper and our SPHINCS+-based solution of comparable security.
| Scheme | qbit security | MakeCredential | GetAssertion | ||
|---|---|---|---|---|---|
| Dilithium2-Hybrid | 547.3 | 1,808.7 | 933.8 | ||
| SPHINCS+ | 129 | 283.4 | 1,595.9 | 0.2 | |
| SPHINCS+ | 129 | 283.7 | 1,791.8 | 0.1 | |
| SPHINCS+ | 130 | 429.2 | 2,687.9 | 0.1 |
| qbit security | MakeCredential | GetAssertion | |||
|---|---|---|---|---|---|
| Dilithium3-Hybrid | 668.3 | 2,861.1 | 1,865.2 | ||
| SPHINCS+ | 193 | 283.2 | 2,099.9 | 0.2 | |
| SPHINCS+ | 193 | 429.6 | 2,751.8 | 0.2 | |
| SPHINCS+ | 195 | 426.3 | 3,967.3 | 0.1 |
| qbit security | MakeCredential | GetAssertion | |||
|---|---|---|---|---|---|
| Dilithium5-Hybrid | 799.2 | 4,029.2 | 2,437.4 | ||
| SPHINCS+ | 258 | 425.7 | 2,803.9 | 0.2 | |
| SPHINCS+ | 258 | 429.4 | 3,406.0 | 0.1 | |
| SPHINCS+ | 258 | 432.2 | 4,075.8 | 0.1 |
As you can see, not only is our SPHINCS+-based approach much more conservative in terms of security assumptions, it also (slightly) outperforms the lattice-based solution. It further avoids complexity introduced through hybridization.
The value shows the standard deviation of the runtime over 1000 runs. Interestingly, the pure-Rust implementation of Dilithium they employed has a huge variance in runtime. This makes sense, as Dilithium runtime is not deterministic since some intermediate values have to be discarded and recomputed when a certain criteria is not met.
If you are interested in more in-depth background, checkout the our paper about the subject.
Conclusion
This was a fun project and we’ve learned a lot about hash-based signatures. The main takeaway for us was: hash-based constructions look weird (where is the involved mathematical construction you need a PhD to truly understand?), but they aren’t. Especially when you resort to SPHINCS+, which is stateless and based on well-understood properties of hash functions. When we first looked at the SPHINCS+ submission to the NIST PQC project, we were annoyed at how many parameter sets they submitted. Now we get it: SPHINCS+ can be aligned for all kinds of stuff. We’re curious to see what else it will be used for!
Security has many facets. To stay on top of things, we do a lot of security research here at Neodyme. Sometimes also quirky projects like this one. Check out our blog if you are interested in more.